Как сделать развертку

От ровного листа до круглой обечайки:

Вальцы с асимметричным расположением валков (рис.11) производят практически полную гибку обечайки.

Наиболее современными являются четырехвалковые машины (рис.12), на которых за один цикл осуществляется вальцовка и подгибка краев. Радиус гибки обечаек проверяют шаблонами. Возможные дефекты вальцовки цилиндрических обечаек приведены на рис.14.

Конусы и переходные элементы в каждой прочности и качестве материала

В дополнении к шишкам и переходным частям, мы также производим раковины и доборные любого рода. Компоненты, которые не могут транспортироваться в одной части из-за их размер, мы производим, насколько это технически возможно в ряде сегментов, которые могут быть собраны на месте для получения готового продукта.

Высокая точность и надежность в технологии формирования — как раз вовремя

В производстве мы уделяем большое внимание выдающемуся качеству и точности. Существует много причин, по которым вам может понадобиться сделать конус с металлической фольгой

Металлические конусы служат для запирания дымовых труб, вплоть до определенных видов огня на открытом воздухе и во время барбекю, а иногда и в декоративных целях. Складывание листа металла проще, чем вы могли ожидать, поэтому не пугайтесь процесса

Введите его полностью, но с осторожностью, конечно

Также способы получения нужной формы бывают разные.

Гибка конических обечаек производится несколькими способами:

1) Установкой под углом среднего валка у симметричных трехвалковых машин и бокового валка у асимметричных трехвалковых и четырехвалковых вальцев (рис.15). 2) Гибкой по средней линии последовательно по различным участкам (рис.16) на вальцах. Сначала осуществляют подгибку кромок, затем гнут середину заготовки на каждом участке с переустановками. Такой способ приводит к повышенному износу оборудования.

3) Гибка обечаек на вальцах со сменными коническими валками. Этот способ оправдан в серийном и массовом производстве. 4) Безвальцевым способом для листа толщиной до 20 мм. На рис. 17 показан метод свертывания. Кромки 3 и 4 заготовки закрепляют в опорах 2 и 5, сводят друг к другу, одновременно поворачивают опоры в разных направлениях. Далее кромки конической обечайки соединяют на прихватках и снимают со станка. 5) Наиболее производительным способом является изготовление конических обечаек в штампах (рис.18). Перед сваркой частей обечаек производят их предварительную фиксацию для исключения деформации элементов и обеспечения сварочных зазоров. Совмещение кромок обычно производится струбцинами и сборочными кольцами для тонкого листа (рис.19). На одну обечайку устанавливается две струбцины по торцам.

Цилиндричность обечаек обеспечивается специальными приспособлениями с домкратами, распирающими деталь. При сборке габаритных деталей используются стяжные планки и клиновые соединения (рис.20).

Изготовление рабочего конуса на заказ

Карандаш будет рисовать круг, и небольшая выемка, которая оставила компас там, где она была поддержана, должна быть отмечена. 2 Отрежьте круг специальными ножницами из металлической фольги. Носите перчатки так, чтобы края металла были очень острыми. 3 Отрежьте круг пополам. Используя точку поддержки вашего компаса в качестве ориентира и в качестве конечной точки, разрежьте там прямую линию, начинающуюся с обоих концов. Теперь у вас будет круг металлической фольги с щелью, которая начнется с одной стороны и достигнет центра. 4 Перекройте одну сторону разреза над другой. Начиная с щели, надавите куски листа один поверх другого. При этом вы увидите, что круг начинает сжиматься и формировать конус. Остановитесь, когда это необходимо, в зависимости от того, насколько глубоко вы этого хотите. 5 Лента на каждой стороне оверлея. Это предотвратит перемещение металла и избавит вас от грубых краев. Теперь ваш конус металлического лезвия завершен. Носите перчатки всякий раз, когда вы манипулируете металлическим лезвием, чтобы не обрезать руки. Металлическое лезвие Ножницы для металлического лезвия Компас с карандашом Клейкая лента Перчатки. Установление определенных единообразных правил находит свое разумное значение в необходимости гарантировать в отношении всех профессий, подверженных сертификации, цели, требующиеся сертификатов профессионализма.

Практическое применение

У школьников часто возникает вопрос о том, зачем учить, как рассчитывать объем разных геометрических тел, в том числе конуса.

А инженеры-конструкторы постоянно сталкиваются с необходимостью рассчитать объем конических частей деталей механизмов. Это наконечники сверл, части токарных и фрезерных станков. Форма конуса позволят сверлам легко входить в материал, не требуя первоначальной наметки специальным инструментом.

Объем конуса имеет куча песка или земли, высыпанная на землю. При необходимости, проведя несложные измерения, можно рассчитать ее объем. У некоторых вызовет затруднение вопрос о том, как узнать радиус и высоту кучи песка. Вооружившись рулеткой, измеряем окружность холмика C. По формуле R=C/2n узнаем радиус. Перекинув веревку (рулетку) через вершину, находим длину образующей. А вычислить высоту по теореме Пифагора и объем не составит труда. Конечно, такой расчет приблизителен, но позволяет определить, не обманули вас, привезя тонну песка вместо куба.

Некоторые здания имеют форму усеченного конуса. Например, Останкинская телебашня приближается к форме конуса. Ее можно представить состоящей из двух конусов, поставленных друг на друга. Купола старинных замков и соборов представляют собой конус, объем которого древние зодчие рассчитывали с удивительной точностью.

Если внимательно присмотреться к окружающим предметам, то многие из них являются конусами:

• воронки-лейки для наливания жидкостей;
• рупор-громкоговоритель;
• парковочные конусы;
• абажур для торшера;
• привычная новогодняя елочка;
• духовые музыкальные инструменты.

Как видно из приведенных примеров, умение рассчитать объем конуса, площадь его поверхности необходимо в профессиональной и повседневной жизни. Надеемся, что статья придет вам на помощь.

Уклон и Конусность

Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.

Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения.
Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.

Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки.

Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали.

Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.

Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона.

Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.

Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах

Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.

Обозначение конусности на чертежах.

Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.

Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.

Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах.
Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.

Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.

Калькуляторы расчета размеров развертки конуса — с пояснениями

Иногда в ходе выполнения тех или иных хозяйственных работ мастер встаёт перед проблемой изготовления конуса – полного или усеченного. Это могут быть операции, скажем, с тонким листовым металлом, эластичным пластиком, обычной тканью или даже бумагой или картоном. А задачи встречаются самый разные – изготовление кожухов, переходников с одного диаметра на другой, козырьков или дефлекторов для дымохода или вентиляции, воронок для водостоков, самодельного абажура. А может быть даже просто маскарадного костюма для ребенка или поделок, заданных учителем труда на дом.

Калькуляторы расчета размеров развертки конуса

Чтобы из плоского материала свернуть объёмную фигуру с заданными параметрами, необходимо вычертить развертку. А для этого требуется рассчитать математически и перенести графически необходимые точные размеры этой плоской фигуры. Как это делается – рассмотрим в настоящей публикации. Помогут нам в этом вопросе калькуляторы расчета размеров развертки конуса.

Несколько слов о рассчитываемых параметрах

Понять принцип расчета будет несложно, разобравшись со следующей схемой:

Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.

Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.

Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.

Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L

Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.

Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:

(Если она уже известна – шаг пропускается)

Перейти к расчётам

Шаг 3 – определение величины центрального угла f

Перейти к расчётам

* * * * * * *

Итак, все данные имеются. Остается на листе бумаги циркулем провести две дуги рассчитанных радиусов. А затем из точки центра с помощью транспортира прочертить два луча под рассчитанным углом – они ограничат развертку по угловой длине.

Существуют и чисто геометрические методы построения довольно точной развертки конуса, без проведения расчётов. Один из них подробно описан в статье нашего портала «Как сделать абажур своими руками».

stroyday.ru

Как построить развертку поверхности прямого усеченного конуса

Делим основание конуса на 12 равных частей (вписываем правильную пирамиду). Данные элементы построения уже готовы из чертежа «Сечение конуса плоскостью частного положения».

Строим развертку боковой поверхности конуса, которая представляет собой круговой сектор. Центр его радиуса принимается за вершину конуса, а величина радиуса кругового сектора конуса равна длине образующей конуса, а длина дуги сектора равна длине окружности основания конуса. На дугу сектора переносим 12 хорд, которые определят ее длину, а также угол кругового сектора.

К центральной точке дуги сектора боковой развертки усеченного конуса пристраиваем основание конуса. Его основание проецируется в натуральную величину на горизонтальную плоскость проекции.

На развертке конуса к его основанию пристраиваем натуральную величину сечения.

Две крайние образующие конуса, которые формируют его основной контур, проецируются на фронтальную плоскость проекции в натуральную величину, поэтому их можно сразу переносить на развертку боковой поверхности конуса. Так как часть его срезана фронтально проецирующей плоскостью, то перенесем на развертку конуса только крайнюю правую усеченную образующую.  Остальные усеченные образующие конуса проецируются на фронтальную плоскость проекций с искажением. Их натуральную величину находят способом вращения вокруг оси конуса до положения, параллельного фронтальной плоскости проекций.

Сам принцип нахождения натуральных величин образующих усеченного конуса сводится к тому, что проводят из точек пересечения образующих с плоскостью горизонтальную прямую до крайней правой (левой) образующей и на ней отмеряют натуральные их величины. Все действия проводят на фронтальной плоскости проекции.

На каждой образующей, лежащей на развертке боковой поверхности конуса, откладываем действительные длины усеченных образующих. Полученные точки соединяем плавной кривой линией команда Сплайн в Автокад.

Мы выполнили задачу начертательной геометрии на построение развертки усеченного конуса, но чтобы не возникло проблем во время ее защиты (когда я обучался, каждая курсовая по начертательной геометрии защищалась), еще раз рассмотрим принцип вращения для нахождения натуральной величины усеченной образующей конуса.

«Их натуральную величину находят способом вращения вокруг оси конуса до положения, параллельного фронтальной плоскости проекций.» Когда мы вращаем образующую прямого конуса до положения параллельного фронтальной плоскости проекции, то ее траектория описывает дугу на горизонтальной плоскости проекции, а на фронтальной прямую!

Вы можете не проводить линии связи с горизонтальной плоскости проекции на фронтальную, ведь очевидно, что точка будет лежать на крайней основной образующей контура конуса для каждой образующей при нахождении ее натуральной величины. Поэтому сам принцип вращения по нахождению натуральной величины образующих конуса сводится к проведению из точек усеченных образующих горизонтальной прямой до основной образующей контура конуса.

В видеоуроке очень наглядно и подробно показан принцип построения развертки прямого усеченного конуса.

Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.

Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения. Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.

Читать также: Сабельная пила для газоблока

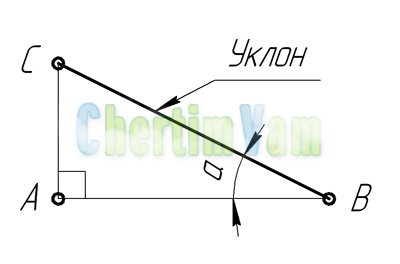
Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.

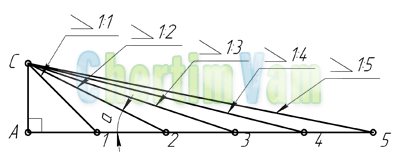
Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.

Задача на определение диаметра через известную площадь конуса и его образующую

Дан конус, площадь поверхности которого составляет 150 см 2 . Генератриса равна 14 см. Чему равен диаметр конуса?

Для получения ответа на поставленный вопрос используем описанную в статье методику. Сначала выпишем соответствующее уравнение:

r 2 + 14*r — 150/3,14 = 0

При получении последнего равенства мы разделили левую и правую его части на число Пи. Рассчитываем дискриминант D. Имеем:

D = 14 2 — 4*1*(-150/3,14) = 387,0828

Полученный дискриминант приведен с точностью до 0,0001. Формула для корней уравнения r имеет следующий вид:

Очевидно, что один из корней будет отрицательным. Его не будем вычислять. Определим лишь искомый положительный радиус фигуры:

r = (-14+√387,0828)/2 = 2,837 см

Чтобы найти диаметр конуса, остается умножить это значение на два и записать ответ: d = 5,674 см.

В конце отметим, что, зная два любых параметра круглого конуса прямого, можно определить любую его характеристику, включая объем и площадь поверхности.

Нормальные углы и конусы инструментов

НОРМАЛЬНЫЕ УГЛЫ ( ГОСТ 8908-81 )

&nbsp Таблица не распространяется на угловые размеры конусов. При выборе углов 1-й ряд следует предпочитать 2-му, а 2-й — 3-му.

НОРМАЛЬНЫЕ КОНУСНОСТИ и УГЛЫ КОНУСОВ ( ГОСТ 8593-81 )

&nbsp Стандарт распространяется на конусности и углы конусов гладких конических элементов деталей.

&nbsp Примечание. Значения конусности или угла конуса, указанные в графе «Обозначение конуса», приняты за исходные при расчете других значений, приведенных в таблице. При выборе конусностей или углов конусов ряд 1 следует предпочитать ряду 2.

КОНУСЫ ИНСТРУМЕНТОВ УКОРОЧЕННЫЕ ( ГОСТ 9953-82 )

&nbsp Стандарт распространяется на укороченные инструментальные конусы Морзе.

&nbsp *z — наибольшее допускаемое отклонение положения основной плоскости, в которой находится диаметр D от теоретическогот положения. &nbsp ** размеры для справок.

КОНУСНОСТЬ НАРУЖНЫХ И ВНУТРЕННИХ КОНУСОВ И КОНУСОВ С РЕЗЬБОВЫМ ОТВЕРСТИЕМ

РЕКОМЕНДУЕМЫЕ РАЗМЕРЫ ЦЕНТРОВОГО ОТВЕРСТИЯ УКОРОЧЕННОГО КОНУСА

КОНУСЫ ИНСТРУМЕНТАЛЬНЫЕ МОРЗЕ И МЕТРИЧЕСКИЕ НАРУЖНЫЕ( ГОСТ 25557-2006 )

&nbsp Профиль резьбового отверстия соответствует отверстию центровому форма Р по ГОСТ ГОСТ 14034-74.

&nbsp В ГОСТ 25557-2006 все размеры центрового отверстия приводятся в общей таблице. Стандарт также определяет размеры пазов канавок и отвестий, необходимых для конструирования конусов, в случае подачи смазочно-охлаждающей жидкости (СОЖ) через инструмент.

&nbsp В зависимости от конструкции инструментальный хвостовик может иметь соответствующее обозначение:

BI — внутренний конус с пазом; BE — наружный конус с лапкой; AI — внутренний конус с отверстием по оси; АЕ — наружный конус с резьбовым отверстием по оси; BIK — внутренний конус с пазом и отверстием для подачи СОЖ; ВЕК — наружный конус с лапкой и отверстием для подачи СОЖ; AIK — внутренний конус с отверстием по оси и отверстием для подачи СОЖ; АЕК — наружный конус с резьбовым отверстием по оси и отверстием для подачи СОЖ.

КОНУСЫ ИНСТРУМЕНТАЛЬНЫЕ МОРЗЕ И МЕТРИЧЕСКИЕ ВНУТРЕННИЕ( ГОСТ 25557-2006 )

КОНУСЫ ВНУТРЕННИЕ И НАРУЖНЫЕ КОНУСНОСТЬЮ 7 : 24 ( ГОСТ 15945-82 )

&nbsp Допуски конусов внутренних и наружных конусностью 7:24 по ГОСТ 19860-93.

КОНУСЫ ИНСТРУМЕНТОВ Предельные отклонения угла конуса и допуски формы конусов ( ГОСТ 2848-75 )

&nbsp Степень точности инструментальных конусов обозначается допуском угла конуса заданной степени точности по ГОСТ 8908-81 и определяется предельными отклонениями угла конуса и допусками формы поверхности конуса, числовые значения которых указаны ниже.

&nbsp Примечания: &nbsp 1. Отклонения угла конуса от номинального размера располагав в «плюс» — для наружных конусов, в «минус» — для внутренних. &nbsp 2. ГОСТ 2848-75 для наружных конусов предусматривает также степени точности АТ4 и АТ5. Допуски по ГОСТ 2848-75 распространяются на конусы инструментов по ГОСТ 25557-2006 и ГОСТ 9953-82.

&nbsp Пример обозначения конуса Морзе 3, степени точности АТ8:

Морзе 3 АТ8 ГОСТ 25557-2006

&nbsp То же метрического конуса 160, степени точности АТ7:

Метр. 160 АТ7 ГОСТ 25557-2006

&nbsp То же укороченного конуса В18, степени точности АТ6:

Морзе В18 АТ6 ГОСТ 9953-82

ГОСТ 2848-75 — Конусы инструментов. Допуски. Методы и средства контроля ГОСТ 7343-72 — Конусы инструментов с конусностью 1:10 и 1:7. Размеры ГОСТ 10079-71 — Развертки конические с коническим хвостовиком под конусы Морзе. Конструкция и размеры ГОСТ 22774-77 — Конусы и трубки шлифовальные. Типы и размеры ГОСТ 25548-82 — Основные нормы взаимозаменяемости. Конусы и конические соединения. Термины и определения

Обозначение конусности на чертеже

При создании технической документации должны учитываться все установленные стандарты, так как в противном случае она не может быть использована в дальнейшем

Рассматривая обозначение конусности на чертежах следует уделить внимание следующим моментам:

1. Отображается диаметр большого основания. Рассматриваемая фигура образуется телом вращения, которому свойственен диаметральный показатель. В случае конуса их может быть несколько, а изменение показателя происходит плавно, не ступенчато. Как правило, у подобной фигуры есть больший диаметр, а также промежуточной в случае наличия ступени.
2. Наносится диаметр меньшего основания. Меньшее основание отвечает за образование требуемого угла.
3. Рассчитывается длина конуса. Расстояние между меньшим и большим основанием является показателем длины.
4. На основании построенного изображения определяется угол. Как правило, для этого проводятся соответствующие расчеты. В случае определения размера по нанесенному изображению при применении специального измерительного прибора существенно снижается точность. Второй метод применяется в случае создания чертежа для производства неответственных деталей.

Простейшее обозначение конусности предусматривает также отображения дополнительных размеров, к примеру, справочную. В некоторых случаях применяется знак конусности, который позволяет сразу понят о разности диаметров.

Выделяют достаточно большое количество различных стандартов, которые касаются обозначения конусности. К особенностям отнесем следующее:

1. Угол может указываться в градусах дробью или в процентах. Выбор проводится в зависимости от области применения чертежа. Примером можно назвать то, что в машиностроительной области указывается значение градуса.
2. В машиностроительной области в особую группу выделяют понятие нормальной конусности. Она варьирует в определенном диапазоне, может составлять 30, 45, 60, 75, 90, 120°. Подобные показатели свойственны большинству изделий, которые применяются при сборке различных механизмов. При этом выдержать подобные значения намного проще при применении токарного оборудования. Однако, при необходимости могут выдерживаться и неточные углы, все зависит от конкретного случая.
3. При начертании основных размеров применяется чертежный шрифт. Он характеризуется довольно большим количеством особенностей, которые должны учитываться. Для правильного отображения используется табличная информация.
4. Для начала указывается значок конусности от которого отводится стрелка и отображается величина. Особенности отображения во многом зависит от того, какой чертеж. В некоторых случаях наносится большое количество различных размеров, что существенно усложняет нанесение конусности. Именно поэтому предусмотрена возможность использования нескольких различных методов отображения подобной информации.

На чертеже рассматриваемый показатель обозначается в виде треугольника. При этом требуется цифровое значение, которое может рассчитываться при применении различных формул.

Создаем новогоднюю елку

Из готового бумажного конуса можно создать отличное новогоднее украшение в виде елочки. Материалы при этом используются самые разнообразные, но общая система изготовления остается общей.

• На бумажный конус наклеивается скотч или пищевая пленка.
• Поверх них, с помощью ПВА или другого подходящего клея, прикрепляются толстые шерстяные нитки.
• После того, как они хорошо засохнут, нужно вынуть из них конус. Нити должны сохранить его форму.
• Останется только добавить элементы для украшения. Это могут быть небольшие вязаные шарики, звездочки из блестящей бумаги или любые другие материалы, оказавшиеся под рукой.

Для создания новогодней елочки можно воспользоваться совершенно другой техникой. На помощь придет папье-маше, с помощью которой можно тоже сделать бумажный конус. Конечно, материала и времени потребуется гораздо больше, но и готовая конструкция получится прочной и статной.

• Для работы потребуются газетные или журнальные обрезки. Подойдет практически любая бумага. Также необходима основа. Можно взять любой пластиковый конус, например – из детских игрушек. Он не пострадает при процессе изготовления.
• Выбранную основу обмазывают ПВА и накладывают на неё слой бумаги. Когда он подсохнет, можно наносить следующий. Таким образом процесс продолжается, пока не наберется достаточная толщина.
• Теперь нужно извлечь основу. Иногда для этого приходится разрезать фигуру.
• Затем вместо основы можно пометить внутрь стержень, который будет выполнять роль каркаса.

Остается лишь склеить разрезанные половинки обратно, и можно приступать к декорированию будущей елки. Например, её реально покрасить или обмотать нитками, как на фото ниже. Такая схема позволит создать любые варианты елочек, в зависимости от желания и имеющейся основы.

Конус по шаблону

Если для будущей поделки вам нужна эта геометрическая фигура, но ни один из вышеперечисленных вариантов, описывающих как сделать нужный конус из бумаги вам не подошел, есть выход.

Что нужно для изготовления:

• плотная бумага;
• ПВА или скотч;
• ножницы;
• карандаш;
• шаблон.

Приступаем к выполнению работы:

• скачиваем шаблон, который мы подготовили и распечатываем его;
• вы можете вырезать по шаблону заготовку или просто сразу использовать материал для конуса и распечатать шаблон на нем;
• сворачиваем материал, края скрепляем удобным для вас способом (скотчем или ПВА клеем).

В процессе скрепления, обязательно следите за тем, чтобы нижние края оставались ровными. Для этого установите еще не собранный материал на стол и уже затем сгибайте. После склеивания. Проверьте ровно ли стоит фигура. Она не должна качаться.