Существует ли треугольник

Виды треугольников

В зависимости от величин углов и соотношения длин сторон различают следующие виды треугольников.

Виды треугольников по углам:

• остроугольные
• прямоугольные
• тупоугольные

Остроугольный треугольник — это треугольник, все углы которого острые (то есть градусная мера каждого угла меньше 90º).

Прямоугольный треугольник — это треугольник, у которого один угол прямой (то есть имеет градусную меру 90º).

Тупоугольный треугольник — это треугольник, у которого один угол — тупой (то есть имеет градусную меру больше 90º).

Виды треугольников по сторонам:

• равносторонние
• равнобедренные
• разносторонние

Равносторонний треугольник (или правильный треугольник) — это треугольник, у которого все три стороны равны.

Равнобедренный треугольник — это треугольник, у которого две стороны равны.

Разносторонний треугольник — треугольник, все стороны которого имеют разную длину.

Если в задаче ничего не сказано о виде треугольника, его считают произвольным, то есть разносторонним.

Отрезки равной длины на чертеже отмечают равным количеством черточек:

разносторонний треугольник

равносторонний треугольник

равнобедренный треугольник

История египетского треугольника

Создателем этой геометрической конструкции является один из величайших математиков древности Пифагор. Именно благодаря его математическим изысканиям мы можем в полной мере использовать все свойства данного геометрического построения в строительстве.

Действительно, есть некоторые египетские рисунки, на которых найден такой инструмент. Имеются данные о том, что пифагорейская теорема была известна также и вавилонянам. Отсюда можно сделать вывод, что они также могли выполнять вычисления с прямоугольным треугольником, по крайней мере в некоторых случаях.

Основываясь на нынешнем уровне знаний об египетской и вавилонской математике и древних греческих источниках, Ван дер-Варден сделал следующий вывод. Достоинство первых греческих математиков, таких как Фалес, Пифагор и Пифагорейцы, — это не открытие математики, а ее систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных идеях, стали наукой.

Можно предположить, что математические навыки позволили Пифагору заметить закономерность в формах строения. Дальнейшее развитие событий можно легко представить. Базовый анализ и построение выводов создали одну из самых значимых фигур в истории. Скорее всего, в качестве прообраза была выбрана именно пирамида Хеопса из-за своих практически совершенных пропорций.

Геометрия у индейцев, а также у египтян и вавилонян была тесно связана с культами. Весьма вероятно, что квадрат гипотенузы был известен в Индии около 18 г. до н.э. Это разные фразы теоремы Пифагора в переводе с древнегреческого, латинского и немецкого языков.

В Евклиде эта теорема гласит. «В прямоугольном треугольнике квадрат стороны пролива над прямым углом равен квадратам сторон, которые фиксируют правый угол». Латинский перевод арабского текста ананиритов был сделан Герхардом Клемонским. «В каждом прямоугольном треугольнике квадрат, сформированный сбоку, нарисованный над прямым углом, равен сумме двух квадратов, сформированных с обеих сторон, покачиваясь под прямым углом».

Стороны египетского треугольника обладают удивительным свойством. Этот удивительный египетский треугольник.

Ка-ж-дый, кто внимательно слушал в школе преподавателя геометрии, очень хорошо знаком с тем, что представляет собой египетский треугольник. От других видов подобных с углом в 90 градусов он отличается особым соотношением сторон. Когда человек впервые слышит словосочетание «египетский треугольник», на ум приходят картины величественных пирамид и фараонов. А что же говорит история?

У Апокалипсиса есть одержимость как ветхозаветными, так и новозаветными библейскими отрывками, фиксация, которая чаще встречается в масонстве, где объединены библейские и египетские идеи. Апокалипсис умирает, говоря «Все раскрывается», что не имеет смысла в фильме, но говорит с аудиторией, говоря, что скрытые знания или секреты масонов выходят из публики и больше не скрываются.

Боб говорит, что Апокалипсис создает пирамиду в современный день, используя свою способность перемещать материю. Способность укладывать материю на молекулярном уровне для формирования любой компоновки или конструкции материи в любой форме или форме, проявленной с помощью современных специальных эффектов, может быть секретом, который он утверждает, «раскрывается», когда он говорит «Все раскрыто». Пирамида и построение сознания Древних Строителей и Масонов должны представлять высший интеллект над звериной природой нормального человечества.

Как это всегда бывает, в отношении названия «египетский треугольник» есть несколько теорий. Согласно одной из них, известная теорема Пифагора увидела свет именно благодаря данной фигуре. В 535 году до н.э. Пифагор, следуя рекомендации Фалеса, отправился в Египет с целью восполнить некоторые пробелы в познаниях математики и астрономии

Там он обратил внимание на особенности работы египетских землемеров. Они очень необычным способом выполняли построение с прямым углом, стороны которой были взаимосвязаны одна с другой соотношением 3-4-5

Данный математический ряд позволял относительно легко связать квадраты всех трех сторон одним правилом. Именно так и возникла знаменитая теорема. А египетский треугольник как раз и есть та самая фигура, натолкнувшая Пифагора на гениальнейшее решение. Согласно другим историческим данным, фигуре дали название греки: в то время они часто гостили в Египте, где могли заинтересоваться работой землемеров. Существует вероятность, что, как это часто бывает с научными открытиями, обе истории произошли одновременно, поэтому нельзя с уверенностью утверждать, кто же придумал первым название «египетский треугольник». Свойства его удивительны и, разумеется, не исчерпываются одним лишь соотношением размеров сторон. Его площадь и стороны представлены целыми числами. Благодаря этому применение к нему теоремы Пифагора позволяет получить целые числа квадратов гипотенузы и катетов: 9-16-25. Конечно, это может быть простым совпадением. Но как в таком случае объяснить тот факт, что египтяне считали «свой» треугольник священным? Они верили в его взаимосвязь со всей Вселенной.

Концептуальное искусство Ральфа МакКуэрри для «Звездных войн» довольно простое, когда оно адаптировано к фильму, но есть одно изображение, которое, как представляется, является видом на землю Облачного города, с городом из трех основных пирамид, окруженных более мелкими пирамидами. Этот образ никогда не попадал в кино.

Как вы можете встать, если вы не на коленях? Исаак Вайшаупт был на переднем крае теорий заговора, связанных с неуловимым «Иллюминатами» и его проникновением в индустрию развлечений. Это исследования теорий с использованием людей и событий в качестве демонстраций. Автор не знает, связаны ли эти люди с этими практиками, а изучает их поведение, чтобы получить теорию. Если кто-то здесь, как утверждается, является частью «Иллюминатов», пожалуйста, не принимайте его как факт, пока вы не выполните собственное исследование.

Правый треугольник имеет один угол, равный 90 градусам. Правый треугольник также может быть равнобедренным треугольником, что означает, что он имеет две стороны, которые равны. Правый равнобедренный треугольник имеет угол 90 градусов и два угла 45 градусов. Это единственный правильный треугольник, который является равнобедренным треугольником. Эта версия правого треугольника настолько популярна, что пластиковые модели из них изготавливаются и используются архитекторами, инженерами, плотниками и художниками-графиками в их проектных и строительных работах.

О египетском треугольнике и его свойствах хорошо известно ещё с древних времён. Эта фигура широко применялась в строительстве для разметки и построения правильных углов.

Египетский треугольник

Смотреть что такое «Египетский треугольник» в других словарях:

• Квадратный миллиметр (мм²) → квадратный метр (м²), метрическая система

  Египетский треугольник — – прямоугольный треугольник с соотношением сторон 3:4:5. Сумма указанных чисел (3+4+5=12) с древних времен использовалась как единица кратности при построении прямых углов с помощью веревки, размеченной узлами на 3/12 и 7/12 ее длины. Применялся… … Словарь строителя

• Египетский треугольник — прямоугольный треугольник с отношением сторон 3:4:5 (сумма чисел 3 + 4 + 5 = 12). Землемеры и архитекторы с глубокой древности пользовались соотношением этих чисел для построения прямых углов с помощью верёвки, размеченной узлами на 3/12 и… … Архитектурный словарь

• Египетский Треугольник — Прямоугольный треугольник с соотношением сторон 3:4:5. Сумма указанных чисел (3+4+5=12) с древних времен использовалась как единица кратности при построении прямых углов с помощью веревки, размеченной узлами на 3/12 и 7/12 ее длины. Применялся в… … Строительный словарь

• лунный египетский треугольник — Треугольник, возникающий в центре большого квадрата, построенного на базе трёх лунных обелисков с отношением сторон 3:4:5, при условии, что вся площадь квадрата разделена на серию прямоугольных треугольников с отношением катетов 1:2. E. Egyptian… … Толковый уфологический словарь с эквивалентами на английском и немецком языках

• Треугольник (значения) — В Викисловаре есть статья «треугольник» Треугольник в широком смысле объект треугольной формы, либо тройка объектов, попарно связ … Википедия

• Треугольник Халаиба — Халаибский треугольник مثلث حلايب спорная территория ← … Википедия

• Египетский крест (астеризм) — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете … Википедия

• Египетский лук — Угловой лук у стрелка на колеснице и простой у пехотинца Египетские луки, как стрелковое оружие прошли определенный путь эволюционного развития от простого из одного вида дерева до сложносоставного («углового») из разных видов… … Википедия

• Халаибский треугольник — مثلث حلايب спорная территория ← … Википедия

• Зимний треугольник — красный цвет = зимний треугольник, синий цвет = зимний круг … Википедия

Цели урока

Познакомиться с новыми определениями и вспомнить некоторые уже изученные.
Углубить знания по геометрии, изучить историю происхождения.
Закрепить теоретические знания учащихся о треугольниках в практической деятельности.
Познакомить учащихся с Египетским треугольником и его применением в строительстве.
Научиться применять свойства фигур при решении задач.
Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
Воспитательные — посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.

Место в строительном мире

С древнейших времен египетский треугольник нашел почетное место в архитектуре и строительстве. Конструкция пирамиды отличается тем, что позволяет создавать здание с совершенно правильными углами без каких-либо дополнительных инструментов.

Задача намного облегчается, если использовать транспортир или треугольник. Но, раньше применялись только шнуры и веревке, разделенные на отрезки. Благодаря отметкам на веревке можно было с точностью воссоздать прямоугольную фигуру. Строителям заменяла транспортир и угольник веревка, для чего отмечали узлами на ней 12 частей и складывали треугольник с отрезками 3,4,5. Прямой угол получался без затруднений. Эти знания помогли создать множество сооружений, в том числе пирамиды.

Интересно, что до древнего Египта, таким способом строили в Китае, Вавилоне, Месопотамии.

Свойства египетской треугольной фигуры подчиняются истине – квадрат гипотенузы равен квадратам двух катетов. Эта теорема Пифагора знакома каждому со школьной поры. Например, умножаем 5х5 и получаем гипотенузу равную числу 25. Квадраты обоих катетов равны 16 и 9, что в сумме дает цифру 25.

Благодаря таким свойствам, треугольник нашел применение в строительстве. Можно взять любую деталь, с целью провести линию прямого направления с условием, что ее длина должна быть кратной пяти. После этого заметить один край и прочертить от него линию кратную четырем, а от другого кратную трем. При этом каждый отрезок должен быть длиной минимум четыре и три. Пересекаясь, они образовывают один прямой угол в 90 градусов. Другие углы равны 53,13 и 36,87 градусам.

Как быть, если строение не подходит под размер 3×4

Понятно, что если стороны дома не подходят под заданный размер, придётся производить вычисления. Но здесь всё не так уж и сложно. К примеру, необходимо построить здание, размеры которого больше. Тогда можно сделать одну стену длиной 12 м, а вторую − 15 м. В этом случае, пользуясь всё той же теоремой Пифагора и особенностями «египетского треугольника», несложно вычислить необходимую длину диагонали (она же гипотенуза), которая будет равна 19,2 м.

ФОТО: fsks.ruВсе углы разметки под фундамент должны быть идеально прямыми – это аксиома

«Египетский треугольник» − это способ разметки, используемый в строительстве с незапамятных времён. И то, что он и сейчас достаточно популярен, говорит о работоспособности метода. Главное – использовать его на полную, а не обходиться только поверхностными знаниями.

ФОТО: tvoidom-msk.ruЛучше потратить немного больше времени и вывести углы фундамента, чем впоследствии получить массу проблем при строительстве и отделке

Египетский треугольник в строительстве. Общие сведения

Зарождение идеи

Идея у математика появилась после путешествия в Африку по просьбе Фалеса, который поставил задачу Пифагору изучить математику и астрономию тех мест. В Египте он среди бескрайней пустыни встретил величественные строения, поразившие его размером, изяществом и красотой.

Надо заметить, что более двух с половиной тысяч лет назад пирамиды были несколько другими – огромными, с четкими гранями. Тщательно изучив могущественные постройки, коих было не мало, так как рядом с великанами, стояли храмы поменьше, построенные для детей, жен и других родственных лиц фараона, это натолкнуло его на мысль.

Благодаря своим математическим способностям, Пифагор сумел определить закономерность в формах пирамиды, а умение анализировать и делать выводы привели к созданию одной из самых значимых теорий в истории геометрии.

Из истории

Знали ли в древнем Египте о геометрии и математике? Конечно да. Жизнь египтян была тесно связана с наукой. Они регулярно пользовались знаниями при разметке полей, создании архитектурных шедевров. Даже существовала своя служба землемеров, которые применяли геометрические правила, занимаясь восстановлением границ.

Название треугольник получил благодаря эллинам, которые нередко бывали в Египте в VII-V вв. до н.э. Считается, что прообразом фигуры стала пирамида Хеопса, отличающаяся совершенными пропорциями. Ее место особенное в истории. Если посмотреть поперечное сечение, то можно отметить два треугольника, у которых угол внутри равняется 51 о 50’.

Сегодня это строение усеченной формы, приобретенной под воздействием времени, высота явно потерялась. Однако, восстановив ее геометричность, можно сделать вывод, что стороны треугольников равны. Получается в основе заложен золотой прямоугольный треугольник.

Однако, следует рассмотреть другую пирамиду – Хефрена, у которой основа как раз-таки прямоугольный треугольник и где угол наклона боковых граней равен 53 о 12 с соотношением катетов 4:3. Это уже так называемый священный треугольник. Для египтян такая фигура сопоставлялась с семейным очагом: катет вертикального положения олицетворял мужчину, основание – представительницу прекрасного пола, а гипотенуза – рождение ребенка от обоих.

Стороны пирамиды Хефрена в соотношении равны 3:4:5, что точно соответствует теореме Пифагора. Значит, можно сделать вывод, что строители уже знали об этой теореме, но не могли ее сформулировать. Хотя, в исторических письменах встречаются следы использования египетского треугольника за много веков даже до Египта. До сегодняшнего дня это загадка, как могли такие знания получить древние египтяне. Понимали ли они чем обладают?

Особенность фигуры к тому же в том, что благодаря подобному соотношению, она является простым и первым Героновым треугольником, так как ее стороны и площадь целочисленные.

Обратное доказательство

Как доказать, что треугольник прямоугольный? Нужно порой исходить от обратного, то есть если сумма квадратов обеих сторон равна квадрату третьей, то треугольник прямоугольный, что подтверждает равенство 3 2 х4 2 =5 2 и значит он действительно прямоугольный.

Таким образом теорема Пифагора стала каноном и фундаментом развития математической науки. Со школьной скамьи каждый ученик знает, что означает выражение «Пифагоровы штаны во все стороны равны».

Интересно, что теорема Пифагора находится в Книге Гиннесса как теорема, обладающая самым большим количеством доказательств, которых примерно 500.

Особенности

Если рассмотреть более детально отличительные особенности египетского треугольника, то можно выделить следующие моменты:

• все стороны и площадь состоят из целых чисел, как говорилось выше;
• согласно теории великого математика, сумма квадратов катетов равна квадрату гипотенузе;
• такой фигурой возможно отмерить прямые углы в пространстве. Это используется в процессе строительства до сих пор;
• не обязательно пользоваться специальными измерительными приборами, подойдут подручные средства, например, веревка.

Египетский треугольник в строительстве

Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.

Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:

Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.

Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.

Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.

Альтернативные способы построить прямой угол на 90 градусов

Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.

Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.

Как получить египетский треугольник при помощи верёвки

Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.

Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.

Как построить угол в 45, 30 и 60 градусов

Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.

Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.

Свойства египетского треугольника широко использовались в строительстве на протяжении почти, что двух с половиной веков. Даже сейчас при недостатке инструментов строители применяют эту открытую ещё Пифагором методику, чтобы добиться ровных прямых углов.

Тату треугольник: фото примеры актуального и современного нательного дизайна

Неповторимость татуировки гарантирует обладательнице только свойственную ей индивидуальность и неповторимость. Выбирая тату треугольника по фото, обязательно старайтесь внести что-то свое, личное в нательное изображение. Нельзя сделать татуировку как под копирку

Важно вложить в нее особый смысл, понятный только вам и вашим близким людям. Тем более, что вы знаете о том, что при выборе необходимо основываться на значение тату треугольника и дополнительных орнаментов

Цветовое решение в данной ситуации тоже играет немаловажную роль. Если вы жизнерадостны, то не стоит выбирать сплошное черное тату с треугольником, а лучше внести живые нотки ярких красок в рисунок, который будет сопутствовать с вами по жизни.

Особенности египетского треугольника

А теперь давайте более подробно остановимся на отличительных особенностях египетского треугольника:

• Во-первых, как мы уже говорили, все его стороны и площадь состоят из целых чисел;

• Во-вторых, по теореме Пифагора нам известно, что сумма квадратов катетов равна квадрату гипотенузе;

• В-третьих, с помощью такого треугольника можно отмерять прямые углы в пространстве, что очень удобно и необходимо при строительстве сооружений. А удобство заключается в том, что мы знаем, что этот треугольник является прямоугольным.

• В-четвертых, как нам тоже уже известно, что даже если нет соответствующих измерительных приборов, то этот треугольник можно запросто построить с помощью простой веревки.

История открытия

Название египетский треугольник получил благодаря эллинам и Пифагору, которые были частыми гостями в Египте. И случилось это приблизительно в VII-V веках до н. э.

Знаменитая пирамида Хеопса, вообще-то представляет собой прямоугольный многоугольник, а вот священным египетским треугольником принято считать пирамиду
Хефрена.

Жители Египта природу Египетского треугольника, как писал Плутарх, сопоставляли с семейным очагом. В их трактовках можно было услышать, что в этой геометрической фигуре ее вертикальный катет символизировал мужчину, основание фигуры относилось к женскому началу, а гипотенузе пирамиды отводилась роль ребенка.

А уже из изученной темы вам хорошо известно, что соотношение сторон этой фигуры равно 3:4:5 и, следовательно, что это нас приводит к теореме Пифагора, так как 32 + 42= 52.

И если учесть, что в основании пирамиды Хефрена лежит египетский треугольник, то можно сделать вывод, народ древнего мира знал знаменитую теорему еще задолго до того, как она была сформулирована Пифагором.

Основной особенностью египетского треугольника, скорее всего, было его своеобразное соотношение сторон, которое было первым и простейшим из Героновых треугольников, так как и стороны, и его площадь имели целые числа.

Применение

Египетский треугольник с древности пользовался популярностью в архитектуре и строительстве.

В основном он использовался тогда, когда строили прямые углы с помощью шнура или веревки, разделенной на 12 частей. По отметкам на такой веревке можно было очень точно создать прямоугольную фигуру, катеты которой будут служить направляющими для установки прямого угла строения. Известно, что такие свойства этой геометрической фигуры использовались не только в Древнем Египте, но и, задолго до этого, в Китае, Вавилоне и Месопотамии. Для создания пропорциональных сооружений в Средние века также использовался египетский треугольник.

Эти предпосылки лежат в основе разработки этой работы, направленной также на создание инструмента для будущих обсуждений возможностей повышения качества преподавания, особенно в области геометрии. Во время строительства учебного плана было отмечено, что можно отказаться от традиционных подходов, начиная с более динамичного и эффективного класса, вызывая интерес и добиваясь обучения студентов.

Изучение содержания по своей сути так же важно, как и приятное, и в те времена, когда мы живем, мы, учителя, можем изменить ситуацию, ища более культурное, организованное и лучше организованное общество. Когда мы начнем думать немного, как гениев прошлого, мы поймем, что они действительно искали в своих открытиях, и полностью поймут содержание, которое они записывают, обеспечивая как понимание учащимися содержания, которое они изучают, так и для нас Это мы учим

Небольшие хитрости

Египетский треугольник 3х4х5 актуален для маленьких домов. Но, что делать, если дом 12х15?

Для этого нужно построить прямоугольный треугольник, у которого катеты равняются 12 и 15 м. Гипотенуза находится как квадратный корень из суммы 12х12 и 15х15. В итоге получаем 19,2 м. С помощью чего-либо — веревки, шпагата, бечевки, тросика, военного кабеля, отмеряем 12, 15 и 19,2 м. Делаем узлы на этих местах и ставим жимки.

Затем треугольник нужно растянуть на нужном месте и установить 3 точки опоры, в которые вбить колышки. Четвертую точку можно получить, не трогая концы катетов. Для этого точка прямого угла перекидывается по диагонали и все готово.

Например, есть участок, где требуется прямой угол – для места под кухонный гарнитур, раскладки кафеля и других моментов. Хорошо бы такие вопросы учесть при кладке, но реальность другая и не всегда попадаются ровные стены и прямые углы. Здесь пригодится египетский треугольник с соотношением 3:4:5, либо при необходимости 1,5:2:2,5.

Обязательно учитывается толщина маяков, погрешность, бугры на стенах и т.д. Треугольник рисуется с помощью рулетки и мела. Если разметка небольшая, то можно воспользоваться листом гипсокартона, так как режутся они с правильными углами.

Египетский треугольник широко использовался в строительстве целых 2,5 века. И сегодня иногда приходится применять данную методику, при отсутствии необходимых инструментов, чтобы получить прямые углы. Свойства этой фигуры уникальны, что гарантирует точность в архитектуре и строительстве, без которой не обойтись. С ним легко работать, по форме он гармоничен и красив. До сих пор пытливые умы пытаются разгадать тайну египетского треугольника.

Доклад по теме «Треугольники в нашей жизни»

по математике на тему:

«Треугольники в жизни человека»

Подготовила: ученица 8 «А» класса

Руководитель: учитель математики

Виноградова Светлана Анатольевна.

Моя работа на тему «Треугольники в жизни человека» призвана доказать, что треугольник и математика с ним окружают нас везде и всегда. Стоит только внимательно присмотреться.

Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Эта фигура встречается везде, но не всегда её замечают.

Равносторонний треугольник символизирует «ЗАВЕРШЕНИЕ».

Треугольник в круге означает мир форм, заключенный в круге вечности.

Существует магическое слово в виде треугольника «Абракадабра». Оно выписывалось столбиком на дощечке 11 раз, при этом последняя буква каждый раз отсекалась. Получался треугольник. Такое постепенное укорачивание этого слова должно было уничтожать силу злого духа, и больной, надевая амулет, должен был постепенно выздоравливать.

Египетские пирамиды тоже в форме треугольника. Пирамида имеет квадрат в плане и треугольник в вертикальном сечении, квадрат соответствует кресту, образованному четырьмя кардинальными точками.

Песочные часы часто появляются в изображении благочестивого, тихого образа жизни, для иллюстрации краткости человеческого бытия, как атрибут Отца-Времени и иногда Смерти. Они разделяют символизм двух треугольников, один из которых перевернут, что означает циклы созидания и разрушения

Треугольники многое значат. Например, равносторонний треугольник свидетельствует об упрямстве, несговорчивости и методичности

В 1934 году шведским художником Оскаром Реутерсвардом была открыта невозможная фигура под названием «Треугольник Пенроуза». В 1980 году этот вариант невозможного треугольника был напечатан на шведских почтовых марках.

В Атлантическом океане есть район, в котором якобы происходят таинственные исчезновения морских и воздушных судов – бермудский треугольник. Район является очень сложным для навигации: здесь большое количество отмелей, часто зарождаются циклоны и штормы. Люди выдвигают различные гипотезы для их объяснения: от необычных погодных явлений до похищений инопланетянами или жителями Атлантиды. Сторонники теории упоминают об исчезновении примерно 100 крупных морских и воздушных судов за последние сто лет. Кроме исчезновений, сообщается об исправных судах, брошенных экипажем, и о других необычных явлениях, таких как мгновенные перемещения в пространстве, аномалии со временем и т. п. Лоуренс Куше и другие исследователи показали, что некоторые из этих случаев произошли за пределами Бермудского треугольника. О некоторых происшествиях вообще не удалось найти никакой информации в официальных источниках.

«Глаз в треугольнике» (или «Всевидящее око», или «сияющая дельта») считается символом Бога. Происхождение свое он ведет с глубокой древности. Возможно, традиция изображать подобным образом божество берет свое начало еще в Древнем Египте. В этом государстве часто использовался религиозный знак «соколиное око Гора». В Древней Индии существовал похожий символ – «третий глаз Шивы».

Знаки дорожного движения тоже состоят из треугольников.

Небольшие хитрости

Египетский треугольник 3х4х5 актуален для маленьких домов. Но, что делать, если дом 12х15?

Для этого нужно построить прямоугольный треугольник, у которого катеты равняются 12 и 15 м. Гипотенуза находится как квадратный корень из суммы 12х12 и 15х15. В итоге получаем 19,2 м. С помощью чего-либо — веревки, шпагата, бечевки, тросика, военного кабеля, отмеряем 12, 15 и 19,2 м. Делаем узлы на этих местах и ставим жимки.

Затем треугольник нужно растянуть на нужном месте и установить 3 точки опоры, в которые вбить колышки. Четвертую точку можно получить, не трогая концы катетов. Для этого точка прямого угла перекидывается по диагонали и все готово.

Например, есть участок, где требуется прямой угол – для места под кухонный гарнитур, раскладки кафеля и других моментов. Хорошо бы такие вопросы учесть при кладке, но реальность другая и не всегда попадаются ровные стены и прямые углы. Здесь пригодится египетский треугольник с соотношением 3:4:5, либо при необходимости 1,5:2:2,5.

Обязательно учитывается толщина маяков, погрешность, бугры на стенах и т.д. Треугольник рисуется с помощью рулетки и мела. Если разметка небольшая, то можно воспользоваться листом гипсокартона, так как режутся они с правильными углами.

Египетский треугольник широко использовался в строительстве целых 2,5 века. И сегодня иногда приходится применять данную методику, при отсутствии необходимых инструментов, чтобы получить прямые углы. Свойства этой фигуры уникальны, что гарантирует точность в архитектуре и строительстве, без которой не обойтись. С ним легко работать, по форме он гармоничен и красив. До сих пор пытливые умы пытаются разгадать тайну египетского треугольника.

Итоги

Свойства египетского треугольника широко использовались в строительстве на протяжении почти, что двух с половиной веков. Даже сейчас при недостатке инструментов строители применяют эту открытую ещё Пифагором методику, чтобы добиться ровных прямых углов.

Синий — по принципу «дуализма» — солнечного сплетения, точка поддержки с расслабленной рукой. Благодаря равенству двух упомянутых групп элементов мы наблюдаем еще одно явление — гармонию между симметрией и асимметрией в одной и той же системе, чередование пассивной и творческой природы. Основные размеры персонала совпадают с очень практическими мерами — например, высота сиденья, высота локтя и пупок человека, высота человека. Значения являются частью линии Фибоначчи, поэтому мы можем легко получить другой желаемый размер.

Он изучал ремесло в Константинополе и Персии. Позже, в Италии, он встречает Гарибальди. К сожалению, никто не смог сохранить этот ключ, через который мы могли бы добраться до многих его секретов: Мое сердце мастера-строителя росло. Что делает мастер, когда он начинает строить дом, церковь или школу?! Обозначает границы конструкции и измеряет прямые углы.

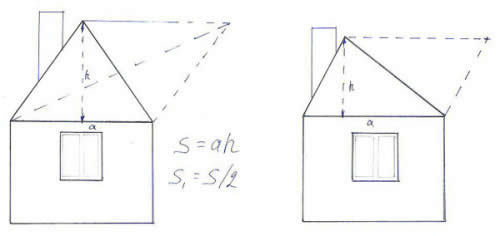
>>Геометрия: Египетский треугольник. Полные уроки